Você está executando um teste em uma das suas páginas de destino com o objetivo principal de fazer com que o usuário clique em um botão. Você está fazendo um teste de (teste A / B) duas cores de botões diferentes (verde e laranja) para determinar o impacto da cor do botão na taxa de cliques. Você obtêm os seguintes resultados iniciais:
| Cor do Botão | Visitantes | Cliques | CTR) |
| Verde | 38 | 2 | 5.2% |
| Laranja | 39 | 3 | 7.7% |
O botão laranja é melhor, certo?
Não necessariamente. Claro, o botão laranja tem uma taxa de cliques de 7,7% (CTR) em comparação com apenas 5,2% para o botão verde. No entanto, o botão laranja só ganhou um clique mais. Se o próximo visitante na página clicar no botão verde, ambas as variantes terão uma CTR de 7.7%, indicando que a cor do botão é irrelevante neste caso.
Aqui está o que acontece se executarmos esta experiência por vários meses com mais de 16.000 visitantes:
| Cor do Botão | Visitantes | Cliques | CTR |
| Verde | 8,238 | 486 | 5.9% |
| Laranja | 7,893 | 734 | 9.3% |
O botão laranja está melhor agora? Claro que sim.
Embora o problema de tomar decisões com base em dados muito pequenos seja uma conclusão incorreta, o problema de coletar muitos dados é um desperdício de tempo, esforço e dinheiro. Embora houvesse poucos dados para determinar que a laranja era melhor na primeira variante, se você tivesse decidido escolher o botão laranja de qualquer maneira, você poderia ter enviado todos os 16.000 visitantes para a página que tinha um CTR de 9,3%. E assim, gerar muito mais vendas/leads/etc.
Então, quantos usuários são necessários para tomar essa decisão? Podemos usar a seguinte equação:
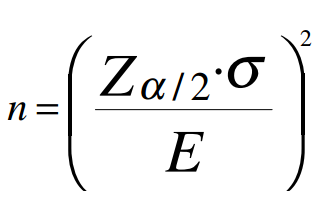 Onde:
Onde:
- n é o tamanho mínimo de amostra necessário para provar que as duas variantes são estatisticamente diferentes.
- Z é o valor correspondente ao intervalo de confiança escolhido na Tabela da Distribuição Normal Padrão. Nas Planilhas do Google pode ser calculado com a fórmula =NORMSINV(x), onde x é a porcentagem de confiança escolhida. Você também pode calcular usando uma tabela de distribuição normal padrão.
- E é tipicamente conhecido como o “erro”. Nesta aplicação, E é a diferença entre os valores médios das duas amostras.
- σ é o desvio padrão.
O escore Z que corresponde a 95% de confiança é 1.64 (da Tabela da Distribuição Normal Padrão).
Por exemplo, digamos que você está usando os dados na segunda tabela acima, e você quer ter confiança de 95% na sua decisão.
E é a diferença entre as duas médias das amostras, então
E = 0,093 (CTR LARANJA) – 0,059 (CTR VERDE)
E = 0,034
Para descobrir o desvio padrão, podemos tratar dados binários como dados contínuos devido ao Teorema do Limite Central, que afirma que, a medida que uma amostra binária aumenta, sua distribuição se aproxima de uma distribuição contínua. Então, determine o CTR geral da seguinte maneira:
CLIQUES TOTAIS = 486 + 734 = 1,220
VISITANTES TOTAIS = 8.238 + 7.893 = 16.135
Isso significa que a taxa de conversão geral foi: 1.220 / 16.135 = 0,0756
No Excel, você pode obter o valor σ usando a função = NORM.S.INV (1-0.0756) que retorna 1,435. Nas planilhas do Google você pode usar a função = =NORMSINV(1-0.0756)
Colocando tudo isso em conjunto, a equação para determinar o tamanho mínimo de amostra necessário para mostrar uma melhoria precisa e estatisticamente significativa do CTR para a página testada com o botão laranja é:
N = ((1,64 * 1,435) / 0,034) ²
N = 4791
Assim sendo. Neste exemplo, você precisará certificar-se de ter 4791 amostras para provar que você tem dados suficientes para tomar uma decisão estatisticamente significativa sobre qual variante é melhor.
- A maioria dos programas de teste A / B cuidarão disso para você. O que você realmente precisa entender sobre a equação é:
- À medida que o desvio padrão aumenta (mais variação na taxa de conversão), você precisará de mais amostras.
- Se quiser mais confiança (95% versus 90%), você precisará de mais amostras.
A medida que a diferença de desempenho entre as duas variantes se torna menor, você precisará de mais amostras (é preciso mais dados para garantir que a diferença não seja apenas o ruído estatístico).
Fácil, certo? Agora, mãos a obra.
Scott Yacko é sócio e co-fundador da Vuurr. Entre seus cargos executivos, ele se define como o especialista de Pay-per-click da Vuurr, alavancando os índices de ROI de seus clientes a niveis extraordinários. Fora de Vuurr, Scott geralmente corre ao ar livre, viajando com sua esposa e brincando com seus cachorros.
Este artigo foi originalmente publicado em inglês como o título: Minimum sample size: How many users is enough?
