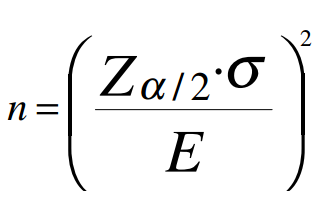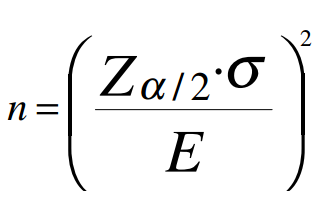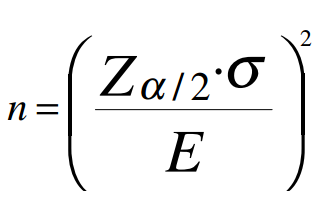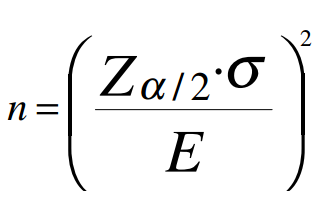
por Scott Yacko | Publicado em Jun 27, 2017 | Marketing
Você está executando um teste em uma das suas páginas de destino com o objetivo principal de fazer com que o usuário clique em um botão. Você está fazendo um teste de (teste A / B) duas cores de botões diferentes (verde e laranja) para determinar o impacto da cor do...